Example
Iris Flowers Species
The following illustrates use of the package to predict the species of flowers in Edgar Anderson’s iris data set.
| Characteristic | Value |
|---|---|
| Number of flowers | 150 |
| Species | |
| setosa | 50 (33.33%) |
| versicolor | 50 (33.33%) |
| virginica | 50 (33.33%) |
| Sepal.Length | |
| Median (Range) | 5.8 (4.3, 7.9) |
| Sepal.Width | |
| Median (Range) | 3 (2.0, 4.4) |
| Petal.Length | |
| Median (Range) | 4.35 (1.0, 6.9) |
| Petal.Width | |
| Median (Range) | 1.3 (0.1, 2.5) |
Training and Test Set Analysis
## Analysis libraries
library(MachineShop)
library(magrittr)
## Training and test sets
set.seed(123)
train_indices <- sample(nrow(iris), nrow(iris) * 2 / 3)
trainset <- iris[train_indices, ]
testset <- iris[-train_indices, ]
## Model formula
fo <- Species ~ .
## Models available for factor responses
modelinfo(factor(0)) %>% names
#> [1] "AdaBagModel" "AdaBoostModel" "BARTModel"
#> [4] "C50Model" "CForestModel" "EarthModel"
#> [7] "FDAModel" "GBMModel" "GLMModel"
#> [10] "GLMNetModel" "KNNModel" "LDAModel"
#> [13] "LMModel" "MDAModel" "NaiveBayesModel"
#> [16] "NNetModel" "ParsnipModel" "PDAModel"
#> [19] "PLSModel" "QDAModel" "RandomForestModel"
#> [22] "RangerModel" "RFSRCModel" "RPartModel"
#> [25] "SelectedModel" "StackedModel" "SuperModel"
#> [28] "SVMModel" "SVMANOVAModel" "SVMBesselModel"
#> [31] "SVMLaplaceModel" "SVMLinearModel" "SVMPolyModel"
#> [34] "SVMRadialModel" "SVMSplineModel" "SVMTanhModel"
#> [37] "TreeModel" "TunedModel" "XGBModel"
#> [40] "XGBDARTModel" "XGBLinearModel" "XGBTreeModel"
## Model-specific information
modelinfo(GBMModel)
#> $GBMModel
#> $GBMModel$label
#> [1] "Generalized Boosted Regression"
#>
#> $GBMModel$packages
#> [1] "gbm"
#>
#> $GBMModel$response_types
#> [1] "factor" "numeric" "PoissonVariate" "Surv"
#>
#> $GBMModel$weights
#> [1] TRUE
#>
#> $GBMModel$na.rm
#> [1] "response"
#>
#> $GBMModel$arguments
#> function (distribution = character(), n.trees = 100, interaction.depth = 1,
#> n.minobsinnode = 10, shrinkage = 0.1, bag.fraction = 0.5)
#> NULL
#>
#> $GBMModel$grid
#> [1] TRUE
#>
#> $GBMModel$varimp
#> [1] TRUE
## Generalized boosted model fit to training set
iris_fit <- fit(fo, data = trainset, model = GBMModel)
## Variable importance
(vi <- varimp(iris_fit))
#> --- VariableImportance object -----------------------------------------------
#> Method: permute
#> Metric: brier
#> Scale: 0.009790379
#> Values:
#> Mean
#> Petal.Length 100.0000000
#> Petal.Width 42.4880573
#> Sepal.Length 4.4254716
#> Sepal.Width 0.4421709
plot(vi)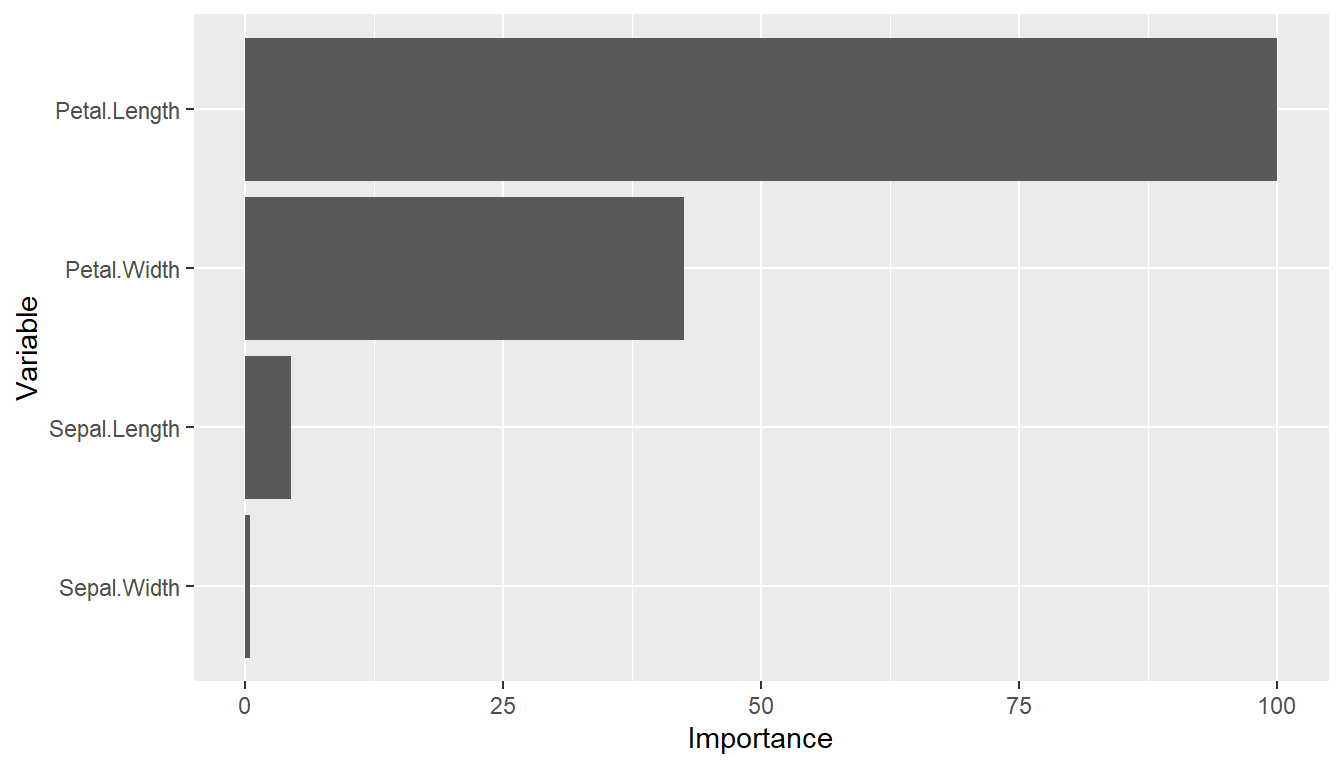
## Test set predicted probabilities
predict(iris_fit, newdata = testset, type = "prob") %>% head
#> setosa versicolor virginica
#> [1,] 0.9999203 7.962238e-05 1.019789e-07
#> [2,] 0.9999804 1.917579e-05 3.924656e-07
#> [3,] 0.9999804 1.917579e-05 3.924656e-07
#> [4,] 0.9999736 2.615002e-05 2.758932e-07
#> [5,] 0.9999015 9.838405e-05 1.019770e-07
#> [6,] 0.9998846 1.153391e-04 1.019753e-07
## Test set predicted classifications
predict(iris_fit, newdata = testset) %>% head
#> [1] setosa setosa setosa setosa setosa setosa
#> Levels: setosa versicolor virginica
## Test set performance
obs <- response(iris_fit, newdata = testset)
pred <- predict(iris_fit, newdata = testset, type = "prob")
performance(obs, pred)
#> Brier Accuracy Kappa ROC AUC
#> 0.07933867 0.96000000 0.93939394 0.99511600Resampling
## Resample estimation of model performance
(res <- resample(fo, data = iris, model = GBMModel, control = CVControl))
#> --- Resample object ---------------------------------------------------------
#>
#> Model: GBMModel
#> Sampling variables:
#> # A tibble: 150 × 2
#> Case Stratification$`(strata)`
#> <chr> <fct>
#> 1 1 setosa
#> 2 2 setosa
#> 3 3 setosa
#> 4 4 setosa
#> 5 5 setosa
#> 6 6 setosa
#> 7 7 setosa
#> 8 8 setosa
#> 9 9 setosa
#> 10 10 setosa
#> # ℹ 140 more rows
#>
#> === CVControl object ===
#>
#> Label: K-Fold Cross-Validation
#> Folds: 10
#> Repeats: 1
summary(res)
#> Statistic
#> Metric Mean Median SD Min Max NA
#> Brier 0.0948393 0.1177027 0.07251105 8.113202e-05 0.2178928 0
#> Accuracy 0.9466667 0.9333333 0.04216370 8.666667e-01 1.0000000 0
#> Kappa 0.9200000 0.9000000 0.06324555 8.000000e-01 1.0000000 0
#> ROC AUC 0.9786667 1.0000000 0.02961481 9.333333e-01 1.0000000 0
plot(res)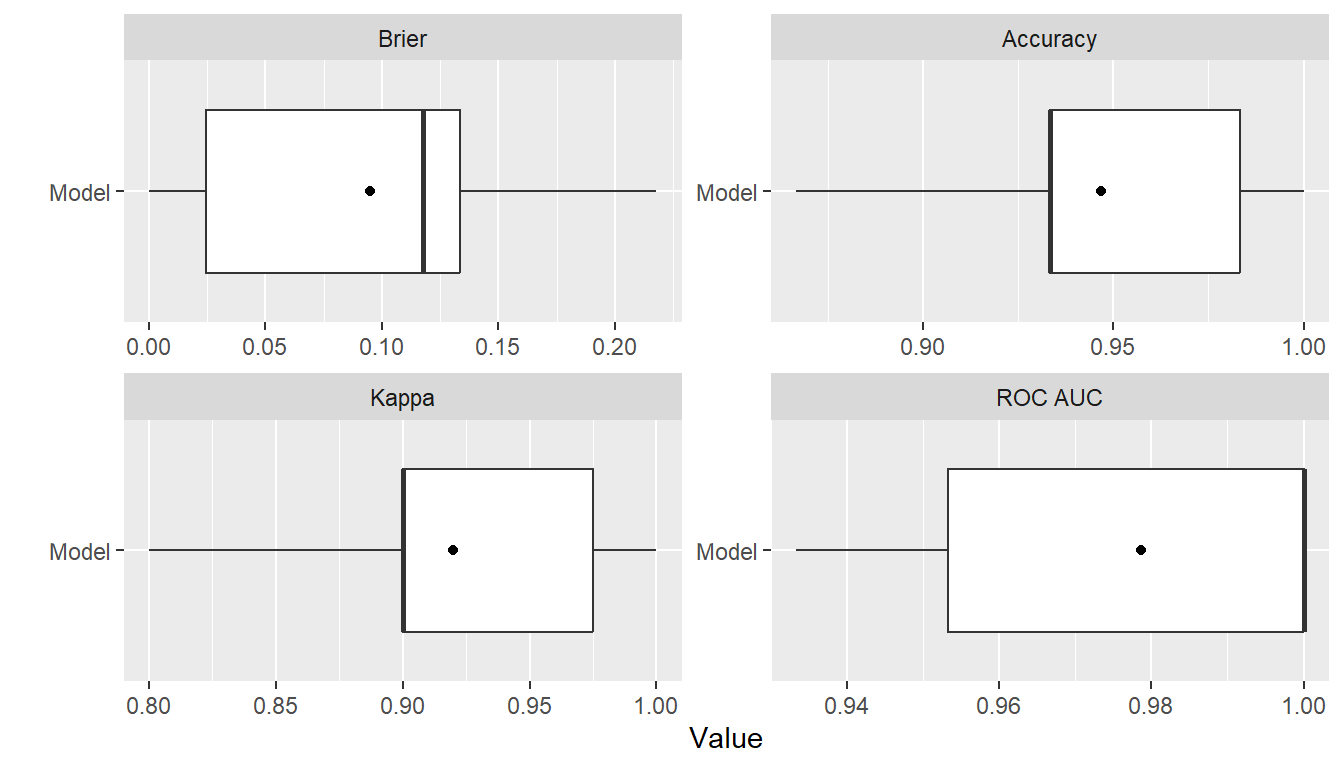
Performance Metrics
## Default performance metrics
performance(res) %>% summary
#> Statistic
#> Metric Mean Median SD Min Max NA
#> Brier 0.0948393 0.1177027 0.07251105 8.113202e-05 0.2178928 0
#> Accuracy 0.9466667 0.9333333 0.04216370 8.666667e-01 1.0000000 0
#> Kappa 0.9200000 0.9000000 0.06324555 8.000000e-01 1.0000000 0
#> ROC AUC 0.9786667 1.0000000 0.02961481 9.333333e-01 1.0000000 0
## Metrics available for the resample output
metricinfo(res) %>% names
#> [1] "accuracy" "auc" "brier" "cross_entropy"
#> [5] "kappa2" "pr_auc" "roc_auc"
## User-specified metrics
performance(res, c(accuracy, kappa2)) %>% summary
#> Statistic
#> Metric Mean Median SD Min Max NA
#> accuracy 0.9466667 0.9333333 0.04216370 0.8666667 1 0
#> kappa2 0.9200000 0.9000000 0.06324555 0.8000000 1 0Model Tuning
## Tune over a grid of model parameters
iris_fit <- TunedModel(
GBMModel,
grid = expand_params(n.trees = c(25, 50, 100),
interaction.depth = 1:3,
n.minobsinnode = c(5, 10))
) %>% fit(fo, data = iris)
## Variable importance
varimp(iris_fit)
#> --- VariableImportance object -----------------------------------------------
#> Method: permute
#> Metric: brier
#> Scale: 0.008658078
#> Values:
#> Mean
#> Petal.Length 100.00000000
#> Petal.Width 24.47878599
#> Sepal.Width 0.11864159
#> Sepal.Length 0.07704569
## Plot performance over the grid points
tuned_model <- as.MLModel(iris_fit)
plot(tuned_model, type = "line")
#> $TrainingStep1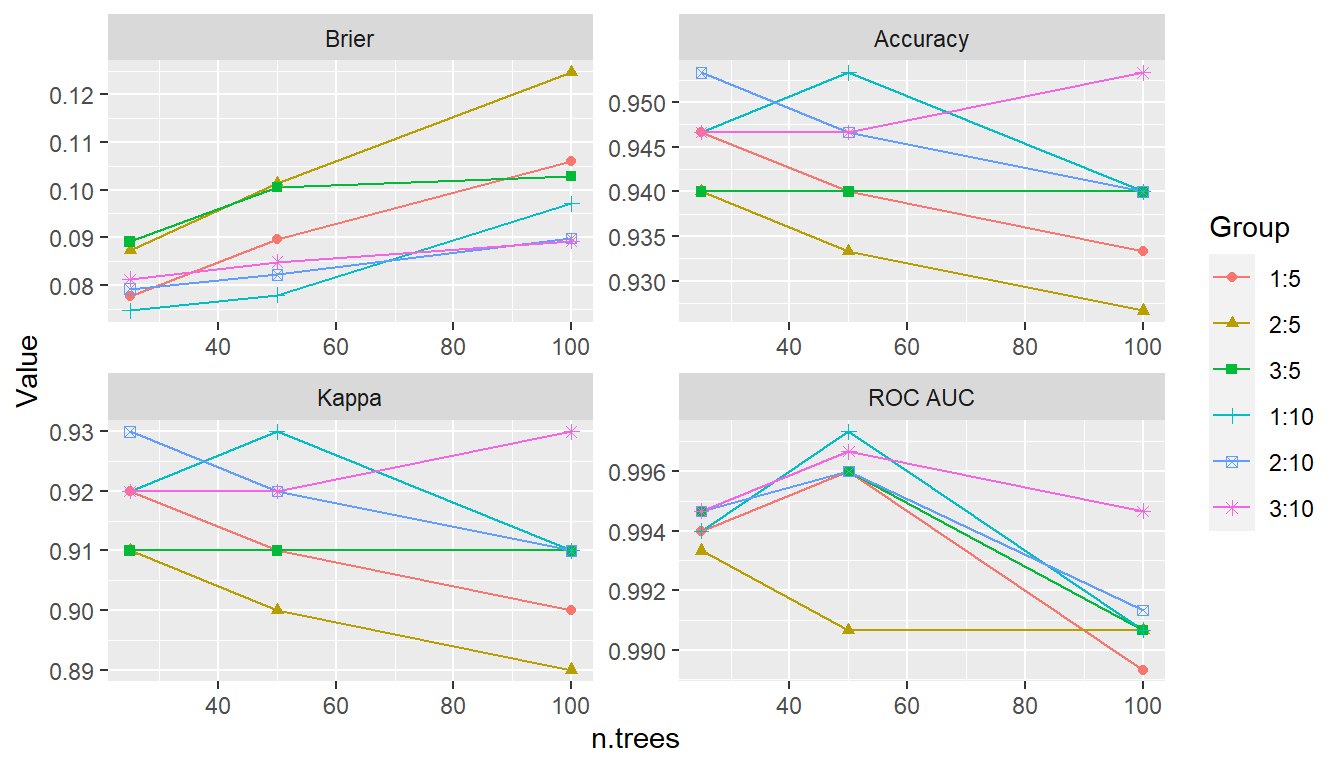
Model Comparisons
## Model comparisons
control <- CVControl(folds = 10, repeats = 5)
res1 <- resample(fo, data = iris, model = GBMModel(n.tree = 50), control = control)
res2 <- resample(fo, data = iris, model = RandomForestModel(ntree = 50), control = control)
res3 <- resample(fo, data = iris, model = NNetModel(size = 5), control = control)
res <- c(GBM = res1, RF = res2, NNet = res3)
summary(res)
#> , , Metric = Brier
#>
#> Statistic
#> Model Mean Median SD Min Max NA
#> GBM 0.08222226 0.07922268 0.08986729 5.358880e-05 0.4860763 0
#> RF 0.06954880 0.05661333 0.07295257 3.733333e-04 0.4088533 0
#> NNet 0.09861942 0.00889123 0.13707365 2.027928e-20 0.6666545 0
#>
#> , , Metric = Accuracy
#>
#> Statistic
#> Model Mean Median SD Min Max NA
#> GBM 0.9506667 0.9333333 0.05183263 0.7333333 1 0
#> RF 0.9533333 0.9333333 0.05429407 0.7333333 1 0
#> NNet 0.9386667 1.0000000 0.09508559 0.6000000 1 0
#>
#> , , Metric = Kappa
#>
#> Statistic
#> Model Mean Median SD Min Max NA
#> GBM 0.926 0.9 0.07774894 0.6 1 0
#> RF 0.930 0.9 0.08144110 0.6 1 0
#> NNet 0.906 1.0 0.15307728 0.4 1 0
#>
#> , , Metric = ROC AUC
#>
#> Statistic
#> Model Mean Median SD Min Max NA
#> GBM 0.9894667 1 0.01919420 0.9333333 1 0
#> RF 0.9932000 1 0.01624584 0.9333333 1 0
#> NNet 0.9722000 1 0.04787365 0.8333333 1 0
plot(res)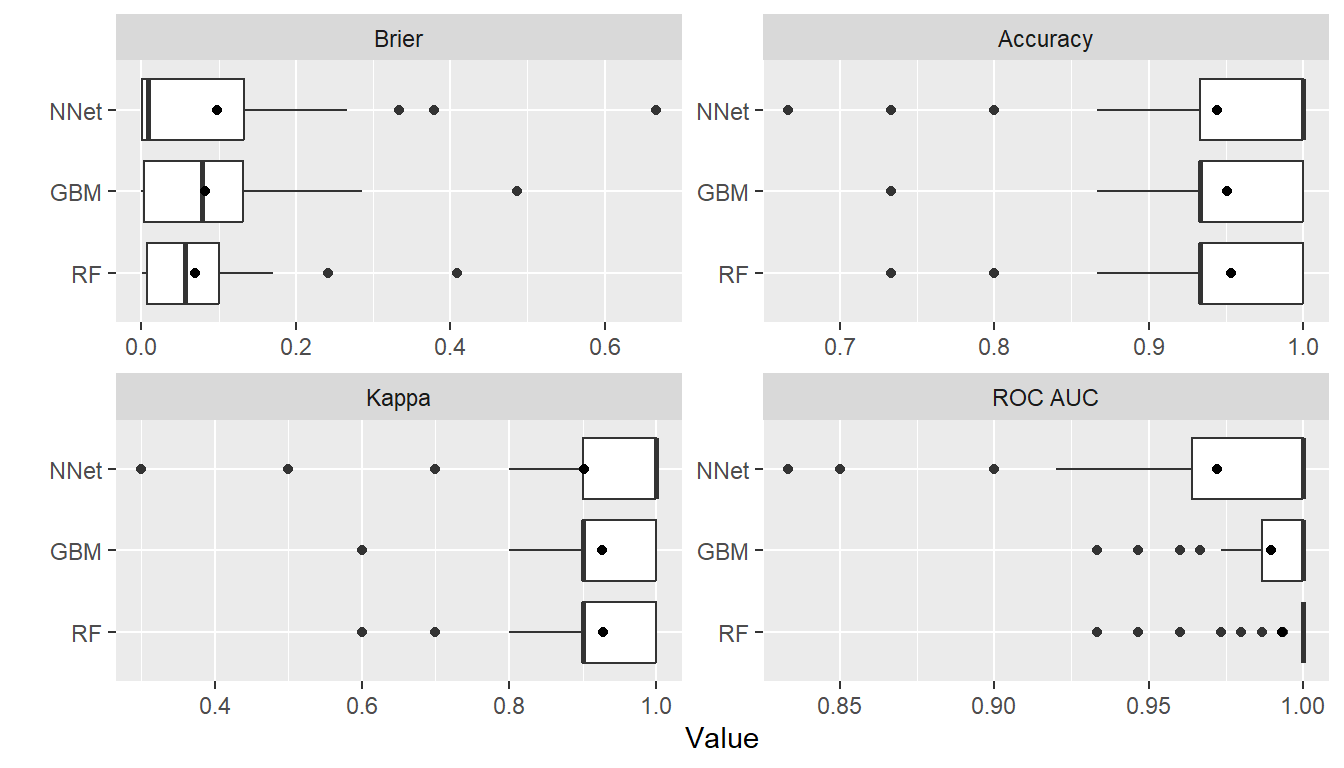
## Pairwise model differences and t-tests
perfdiff <- diff(res)
summary(perfdiff)
#> , , Metric = Brier
#>
#> Statistic
#> Model Mean Median SD Min Max NA
#> GBM - RF 0.01267346 4.261331e-04 0.02768193 -0.02764053 0.07722295 0
#> GBM - NNet -0.01639716 -7.783568e-05 0.10176021 -0.33292223 0.16154038 0
#> RF - NNet -0.02907062 3.669109e-04 0.10357991 -0.33226667 0.11246802 0
#>
#> , , Metric = Accuracy
#>
#> Statistic
#> Model Mean Median SD Min Max NA
#> GBM - RF -0.004 0 0.02487155 -0.06666667 0.06666667 0
#> GBM - NNet 0.008 0 0.07576069 -0.06666667 0.33333333 0
#> RF - NNet 0.012 0 0.07338897 -0.06666667 0.33333333 0
#>
#> , , Metric = Kappa
#>
#> Statistic
#> Model Mean Median SD Min Max NA
#> GBM - RF -0.004 0 0.03475864 -0.1 0.1 0
#> GBM - NNet 0.012 0 0.11890658 -0.1 0.5 0
#> RF - NNet 0.016 0 0.11668902 -0.1 0.5 0
#>
#> , , Metric = ROC AUC
#>
#> Statistic
#> Model Mean Median SD Min Max NA
#> GBM - RF -0.003733333 0 0.01152027 -0.04000000 0.01333333 0
#> GBM - NNet 0.017266667 0 0.04738844 -0.05333333 0.16666667 0
#> RF - NNet 0.021000000 0 0.04690053 -0.06666667 0.16666667 0
t.test(perfdiff)
#> --- PerformanceDiffTest object ----------------------------------------------
#>
#> Upper diagonal: mean differences (Model1 - Model2)
#> Lower diagonal: p-values
#> P-value adjustment method: holm
#>
#> , , Metric = Brier
#>
#> Model2
#> Model1 GBM RF NNet
#> GBM NA 0.01267346 -0.01639716
#> RF 0.6362196 NA -0.02907062
#> NNet 0.8840076 0.88400758 NA
#>
#> , , Metric = Accuracy
#>
#> Model2
#> Model1 GBM RF NNet
#> GBM NA -0.004 0.008
#> RF 1 NA 0.012
#> NNet 1 1.000 NA
#>
#> , , Metric = Kappa
#>
#> Model2
#> Model1 GBM RF NNet
#> GBM NA -0.004 0.012
#> RF 1 NA 0.016
#> NNet 1 1.000 NA
#>
#> , , Metric = ROC AUC
#>
#> Model2
#> Model1 GBM RF NNet
#> GBM NA -0.003733333 0.01726667
#> RF 0.6664138 NA 0.02100000
#> NNet 0.6664138 0.666413775 NA
plot(perfdiff)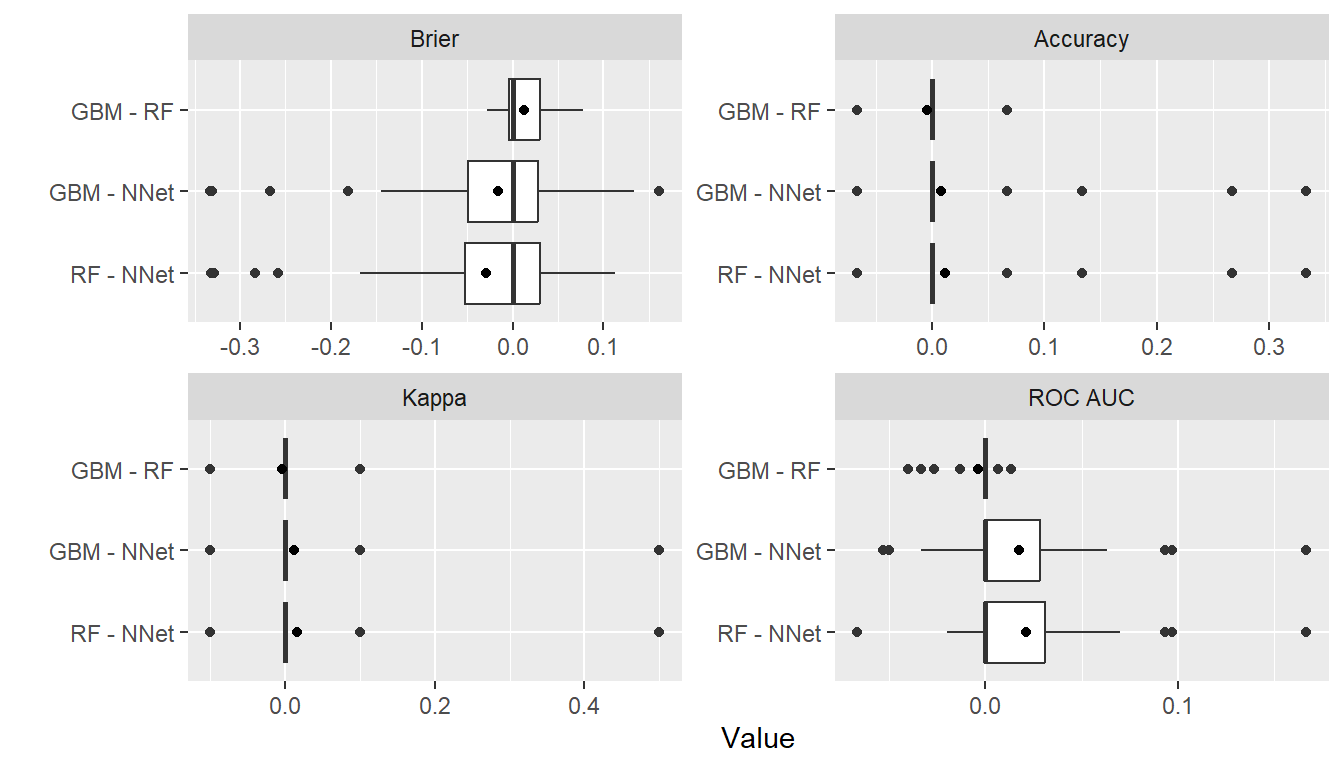
Ensemble Models
## Stacked regression
stackedmodel <- StackedModel(GBMModel, RandomForestModel, NNetModel)
res_stacked <- resample(fo, data = iris, model = stackedmodel)
summary(res_stacked)
#> Statistic
#> Metric Mean Median SD Min Max NA
#> Brier 0.07818532 0.02915482 0.09773153 0.0006731487 0.3006319 0
#> Accuracy 0.95333333 1.00000000 0.07062333 0.8000000000 1.0000000 0
#> Kappa 0.93000000 1.00000000 0.10593499 0.7000000000 1.0000000 0
#> ROC AUC 0.99333333 1.00000000 0.01133115 0.9733333333 1.0000000 0
## Super learner
supermodel <- SuperModel(GBMModel, RandomForestModel, NNetModel)
res_super <- resample(fo, data = iris, model = supermodel)
summary(res_super)
#> Statistic
#> Metric Mean Median SD Min Max NA
#> Brier 0.09363295 0.0773554 0.08677424 1.272903e-06 0.2458399 0
#> Accuracy 0.94666667 0.9666667 0.06885304 8.000000e-01 1.0000000 0
#> Kappa 0.92000000 0.9500000 0.10327956 7.000000e-01 1.0000000 0
#> ROC AUC 0.98800000 1.0000000 0.02126842 9.333333e-01 1.0000000 0Calibration Curves
cal <- calibration(res1)
plot(cal, se = TRUE)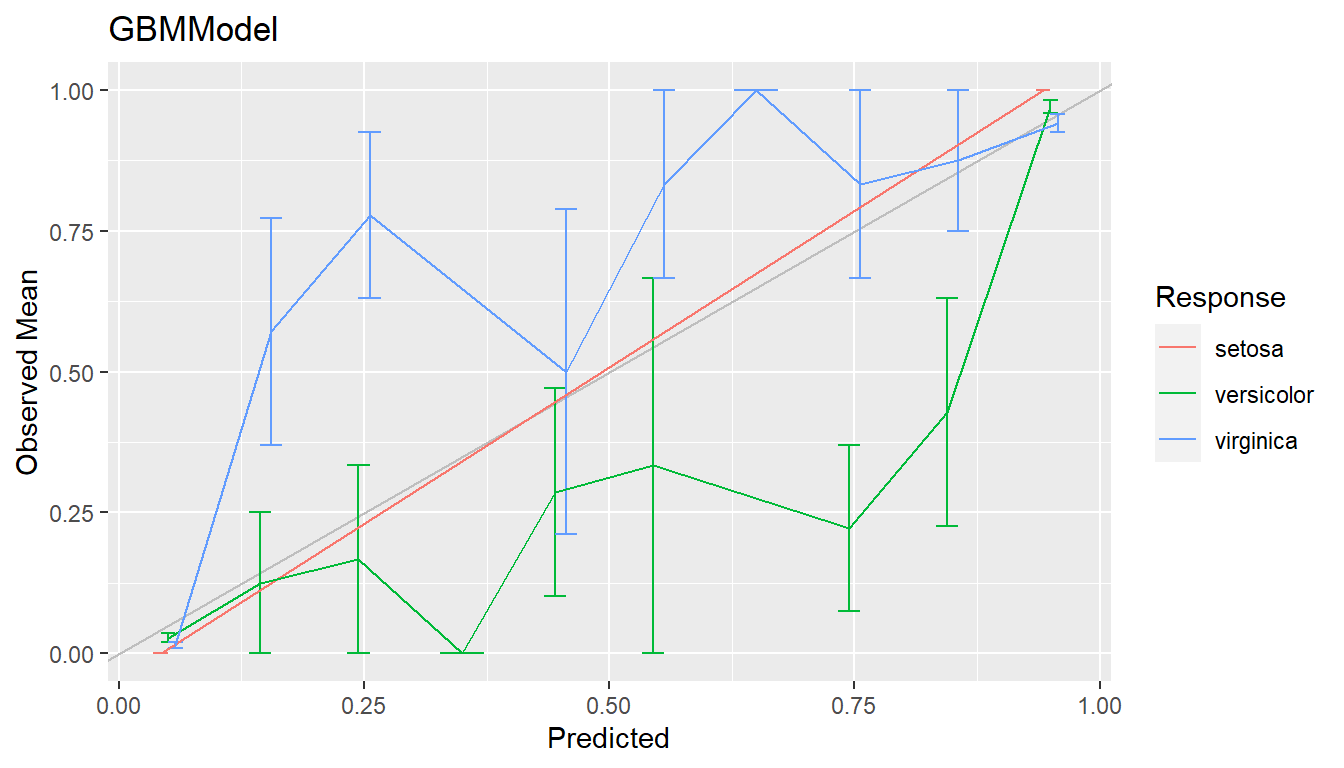
Confusion Matrices
(conf <- confusion(res1, cutoff = NULL))
#> --- ConfusionList object ----------------------------------------------------
#>
#> === $GBMModel ===============================================================
#> === ConfusionMatrix object ===
#> Observed
#> Predicted setosa versicolor virginica
#> setosa 249.30932795 0.25221814 0.09391384
#> versicolor 0.67430045 230.21683206 24.30257249
#> virginica 0.01637160 19.53094980 225.60351367
summary(conf)
#> --- $GBMModel ---------------------------------------------------------------
#> Number of responses: 750
#> Accuracy (SE): 0.9401729 (0.008660086)
#> Majority class: 0.3333333
#> Kappa: 0.9102593
#>
#> setosa versicolor virginica
#> Observed 0.3333333 0.3333333 0.3333333
#> Predicted 0.3328739 0.3402583 0.3268678
#> Agreement 0.3324124 0.3069558 0.3008047
#> Sensitivity 0.9972373 0.9208673 0.9024141
#> Specificity 0.9993077 0.9500463 0.9609054
#> PPV 0.9986136 0.9021258 0.9202641
#> NPV 0.9986196 0.9600184 0.9516757plot(conf)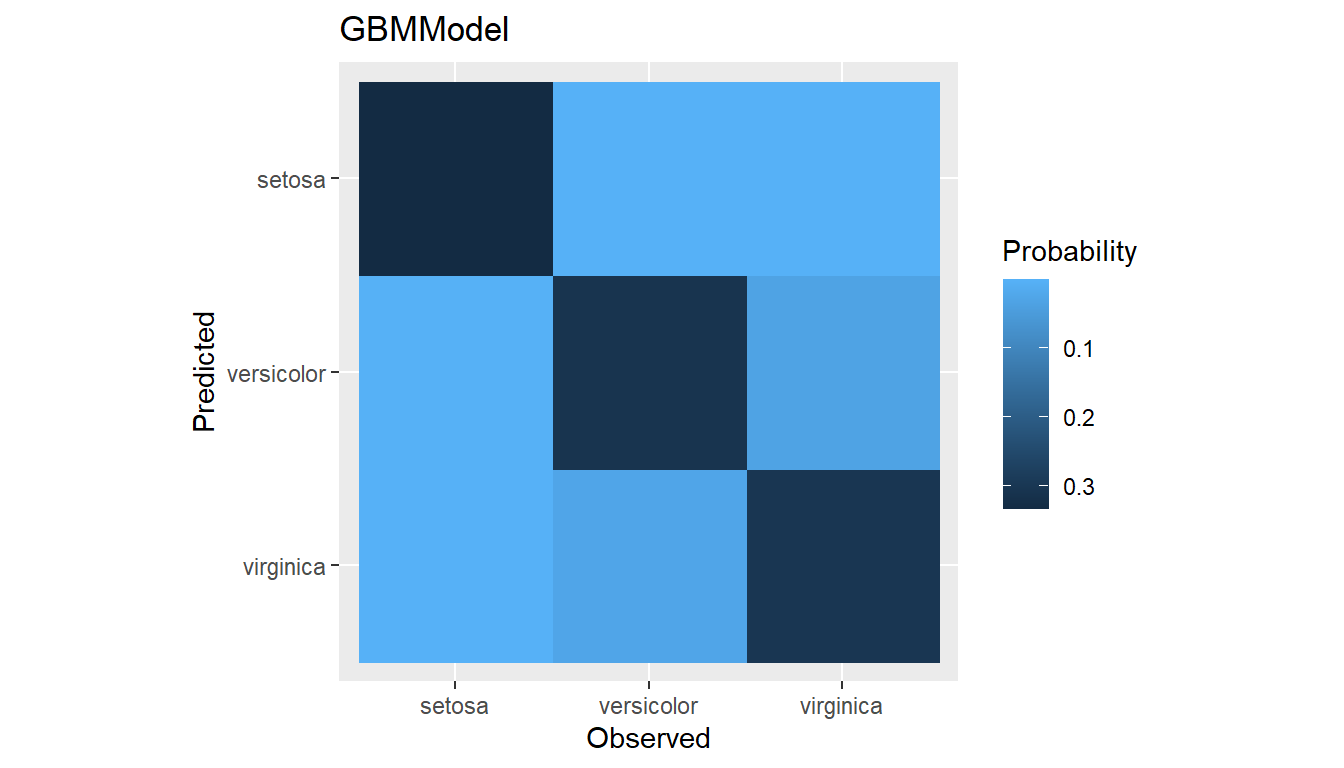
Partial Dependence Plots
pd <- dependence(iris_fit, select = c(Petal.Length, Petal.Width))
plot(pd)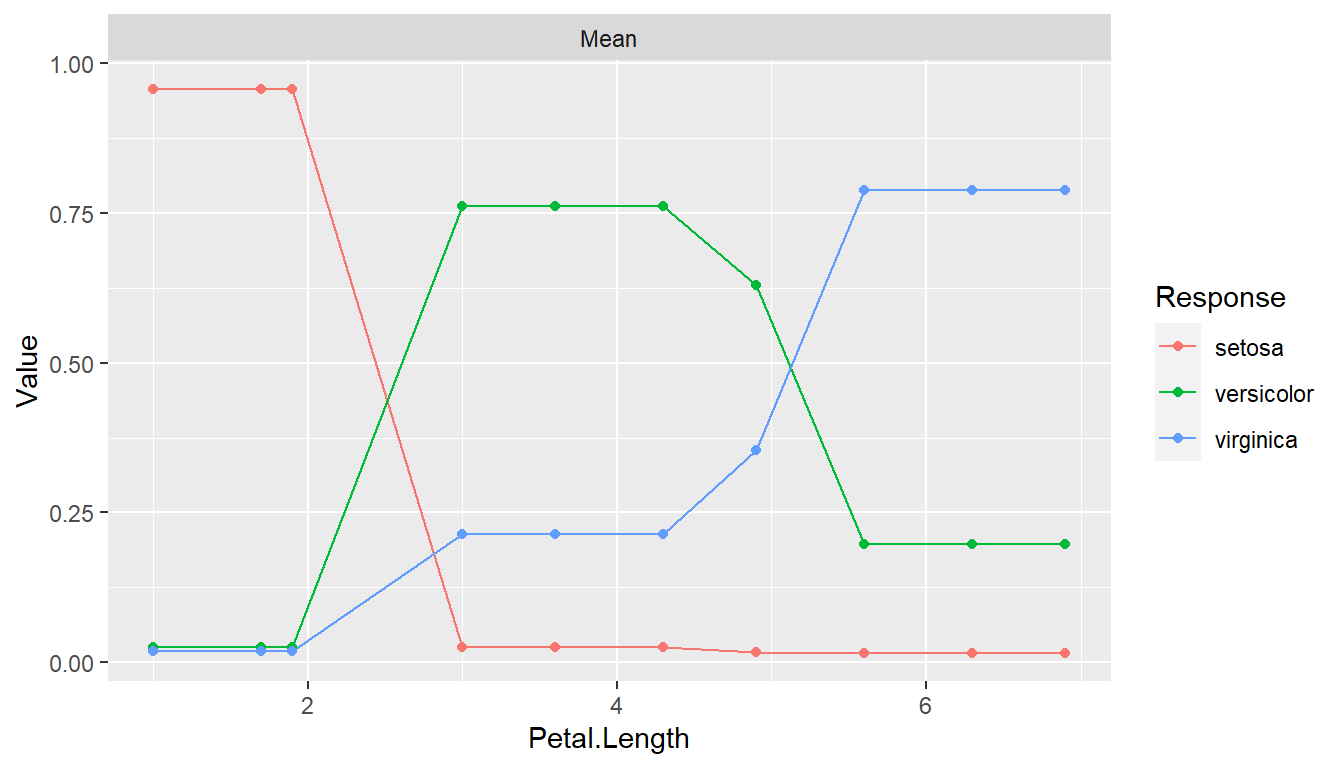
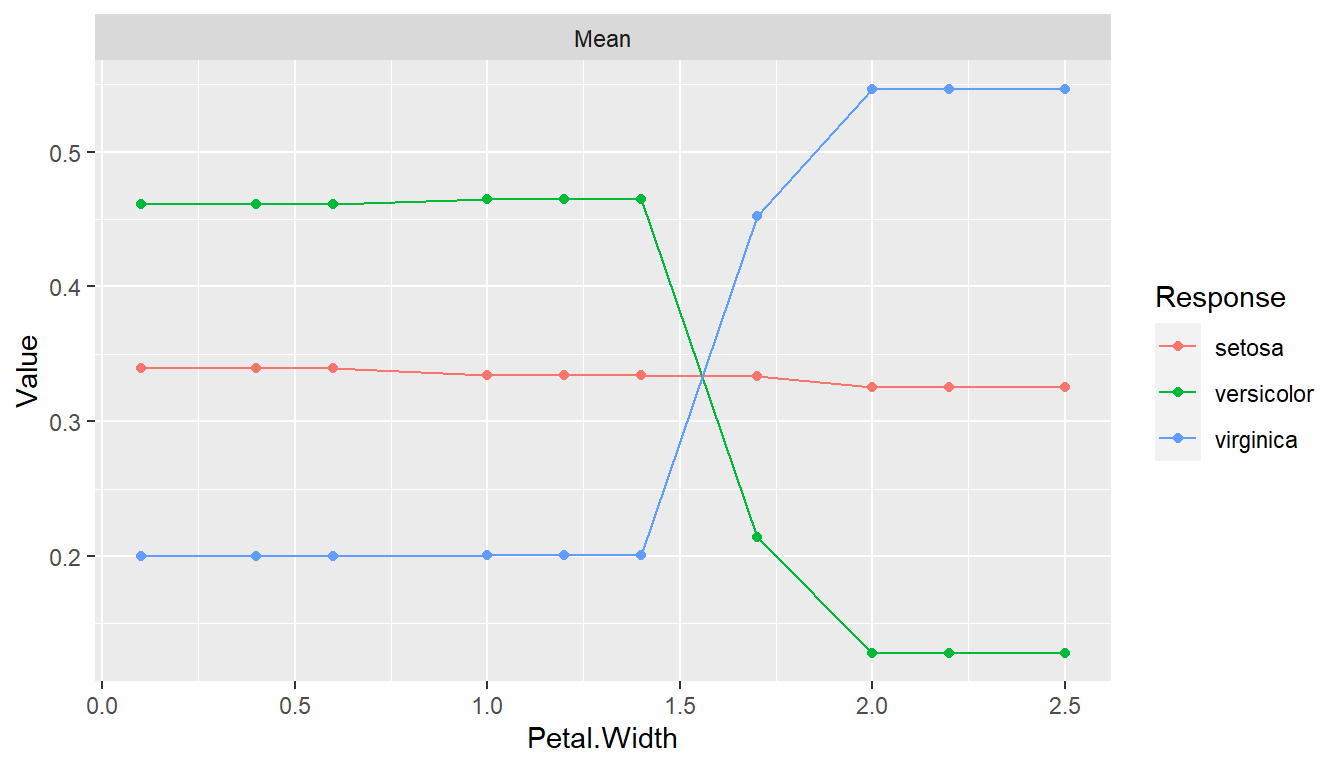
Preprocessing Recipe
library(recipes)
rec <- recipe(fo, data = iris) %>%
role_case(stratum = Species)
iris_fit <- fit(rec, model = GBMModel)
varimp(iris_fit)
#> --- VariableImportance object -----------------------------------------------
#> Method: permute
#> Metric: brier
#> Scale: 0.0108775
#> Values:
#> Mean
#> Petal.Length 100.000000
#> Petal.Width 26.116233
#> Sepal.Width 3.552549
#> Sepal.Length 2.700857
res <- resample(rec, model = GBMModel, control = CVControl)
summary(res)
#> Statistic
#> Metric Mean Median SD Min Max NA
#> Brier 0.1066633 0.08803549 0.13007118 2.811413e-05 0.407564 0
#> Accuracy 0.9333333 0.93333333 0.08314794 7.333333e-01 1.000000 0
#> Kappa 0.9000000 0.90000000 0.12472191 6.000000e-01 1.000000 0
#> ROC AUC 0.9813333 1.00000000 0.02606734 9.333333e-01 1.000000 0